Distance-Based Camera Trigger - Part 1
Remember back when this site had projects on it? I could say that it's because I started a new job or that I started a large-scale ongoing side project that I will hopefully be able to write about, but mostly the reason is because the latest projects have been failures. I've been rushing into too many simultaneous, unnecessary projects too quickly. I also keep forgetting to factor in the small amount of room I have to do these projects.
I took a few pictures with my camera remote recently. I decided that I don't like having the wire connecting it to my camera in every shot. It's time to build a wireless remote. If I'm going to buy parts, I should pre-plan other things I will need for future projects to avoid extra shipping charges. The only thing I really want for my R.C. Tank (yes, I will finish it one day) is an accelerometer. Because I have to write a driver for the accelerometer anyway, why not test it with my new remote?
I will make what is essentially a stop-motion video of my drive to work. I will rig my camera to face out the windshield from the passenger's seat. The trigger would release the shutter every distance D, e.g. every tenth of a mile, along my commute.
Requirements
- Take as many pictures as possible. Limiting factors:
- shutter speed
- memory card write speed
- memory card capacity
- maximum accelerometer bandwidth
- maximum driving speed
- 1x accelerometer
- Only one dimension (forward/backward) is required.
- 1x transmitter/receiver pair
- Communication is only needed in one direction
Theory
I want to determine the amount of distance I travel. However, there is no "distance-ometer." Instead, I have to create one using other components. The only commonly-available component that can help me determine linear motion (as opposed to rotational motion) is an accelerometer. They are relatively cheap but require a little bit of math. Luckily, the required calculus is pretty simple.
Wait... Simple Calculus?
Yes. I'm not claiming that the needed calculus (integration) is simple, but when using digital signals it's greatly simplified. It only requires finding the area of a couple of rectangles (length multiplied by width) and adding them together. Calculus becomes the geometry that you learn before you learn what the word "geometry" even means.
The Physics/Calculus
When anything is moving, such as a car driving, two things can be easily measured by people: distance and time. All other aspects are derived from those two numbers. Let's say I drove 60 miles, and it took me two hours to get there.

If I drive an average speed of 30 MPH for 2 hours, then I will have driven 60 miles (30 x 2 = 60). Speed is the rate of change in the distance with respect to time. Rather than 30 miles/hour, I could have said 0.5 mile/minute, 1/120 mile/second, or 158400 feet/hour. All are equivalent, but it must be distance over time.
Let's plot out speed against time. The function is:
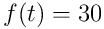
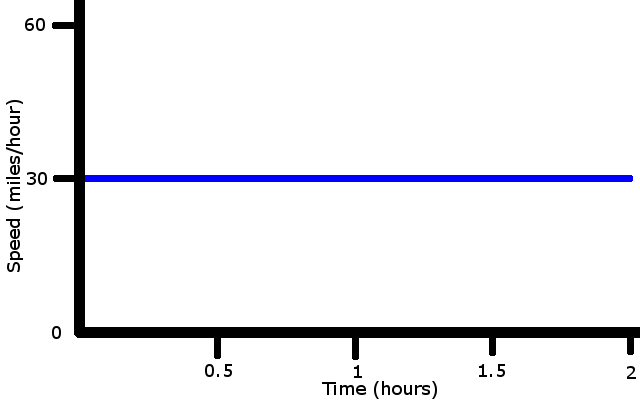
To find out how far the car has traveled, find the area under the line i.e. multiply the width and length of the rectangle.

30 miles/hour * 2 hours = 60 miles
Using the graph, we can find how far we traveled in 1 hour. Draw a line up from the 1 hour mark.
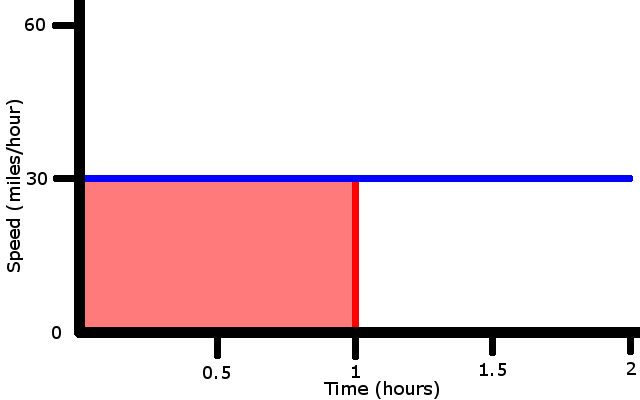
30 miles/hour * 1 hour = 30 miles
So, moving at a constant speed isn't very interesting. Let's travel 1.5 hours at 25 miles/hour, then 0.5 hour at 45 miles/hour.
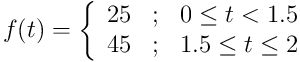
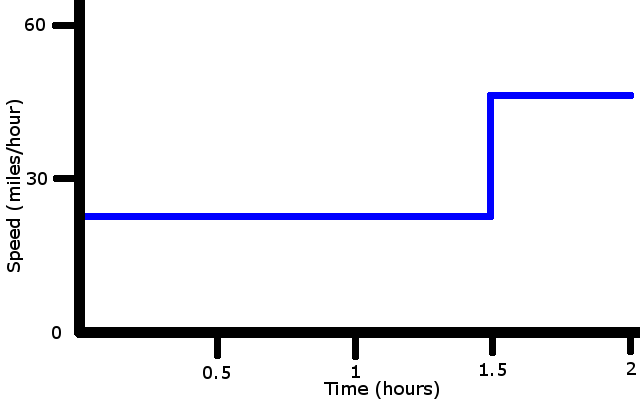
So, how far did the car move in an hour?
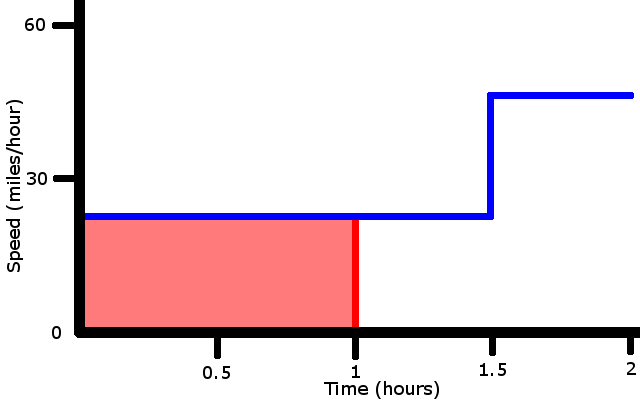
25 miles/hour * 1 hour = 25 miles
How far in 2 hours, then?
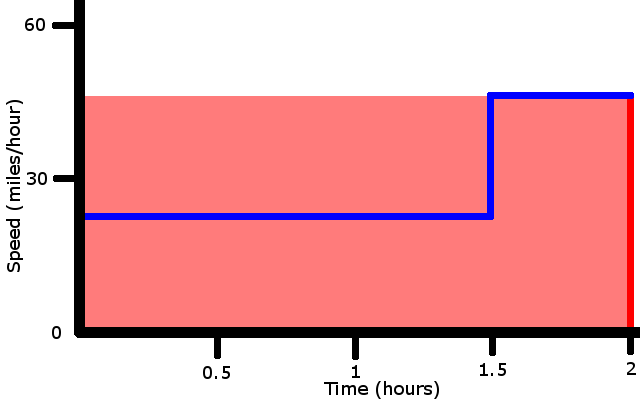
45 miles/hour * 1 hour = 90 miles
Obviously, that's wrong. We're going to have to break this into pieces.
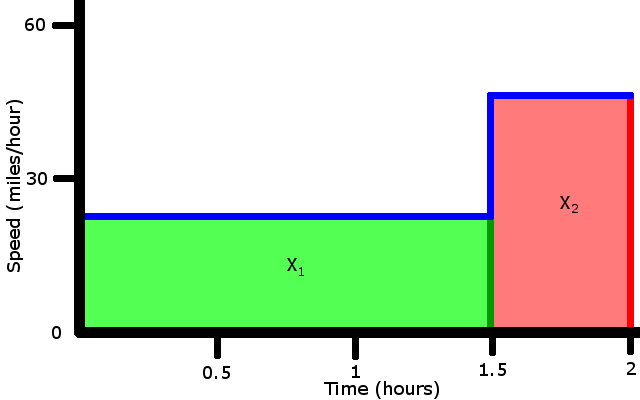
25 miles/hour * 1.5 hours + 45 miles/hour * 0.5 hour = 60 miles
The scary math way of writing this is, where A is the area of each piece:
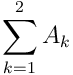
How would we determine the distance from a more realistic line?
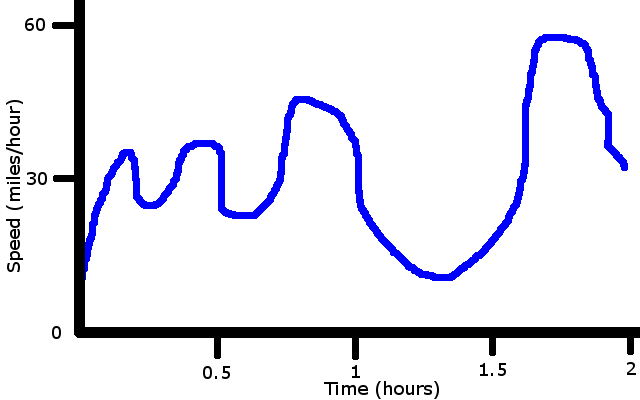
There aren't any obvious pieces. So, we take pieces that are as small as possible. If T is the time between each sample and t is the time of each sample was taken:
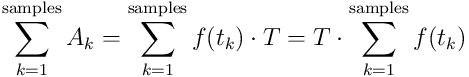
Unnecessary note: If you take an infinite number of samples of infinitely small width, it is called integration.
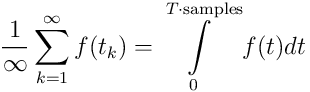
The Method
To calculate distance from speed, multiply each speed sample by the time period between each sample and add them all together. A negative speed is moving in reverse.
To calculate speed, do the same thing with acceleration; multiply each acceleration sample by the time period between each sample and add them all together.
Because I will have an accelerometer, the method will be to collect acceleration sample points as fast as possible and convert it to distance.
->acceleration -> speed -> distance<-
Every time I hit a certain distance, the device will tell my camera to take a picture.
In the next part, I'll show the threshold calculations and more accelerometer information.
